Pythagoras theorem applies to a triangle with lengths a, b and c as shown in diagram.
It indicates that the square of the hypotenuse is equal to the sum of the squares of the other two sides
If you look at the diagram, this means that a² + b² = c²

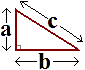
The table below indicates some of the "integer" values that obey the rule and form right-angled triangles.

3	4	5	and all multiples e.g.	6	8	10
5	12	13	and all multiples e.g.	10	24	26
7	24	25	and all multiples e.g.	14	48	50
8	15	17	and all multiples e.g.	16	30	34
9	40	41	and all multiples e.g.	18	80	82
12	35	37	and all multiples e.g.	24	70	74
20	21	29	and all multiples e.g.	40	42	58

Pythagoras theorem can be extended for trianglular prisms with lengths a, b c, and diagonal d as shown in diagram.
It indicates that the square of the diagonal is equal to the sum of the squares of the three main edges
If you look at the diagram a² + b² + c² = d²

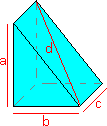
The table below indicates some of the "integer" values that obey the rule and form right-angled prisms.

1	2	2	3
1	4	8	9
2	4	4	6
2	3	6	7
2	6	9	11
3	6	6	9
4	4	7	9
4	8	8	12
5	10	10	15
6	6	8	11

There are very complex mathematical theories as to whether any set of integers exist which could fulfil the equation ...... a³ + b³ = c³
However, integer solutions for extended version of the cubic equation ...... a³ + b³ + c³= d³ ...... include

1	6	8	9
2	12	16	18
3	4	5	6
3	10	18	19
4	3	5	6
5	3	4	6
6	1	8	9
6	8	10	12
7	14	17	20
8	1	6	9
8	6	10	12
9	12	15	18
10	3	18	19
10	8	6	12
12	2	16	18
12	15	9	18
12	16	20	24
14	7	17	20
15	9	12	18
16	2	12	18
16	12	20	24
17	7	14	20
18	3	10	19
20	12	16	24